티스토리 뷰
<숫자의 탄생>에서 가려 뽑은 숫자 상식 3
손가락으로 100억을 헤아리고 곱셈도 가능하다?
숫자는 어디서 온 걸까? 옛날에는 어떻게 셈을 했을까? 누가 0을 발명했을까?
어느 날 문득 이런 궁금증이 든 적이 있었나요? 그렇다면 <숫자의 탄생>을 펼치십시오.
현대인에게 숫자 혹은 셈 능력은 말하기나 걷기처럼, 매일 숨을 쉬면서도 인식하지 못하는 공기처럼 자연스럽지만, 사실 ‘숫자’는 인류 최고의 발명품이자 전 세계적으로 하나의 기수법으로 통일된 ‘진실로 유일한 세계어’입니다.
<숫자의 탄생>은 우리를 시대와 문명을 가로지르는 환상적인 숫자 여행으로 안내합니다. 수학은 싫어해도 수의 역사를 훑어나가며 인류의 모습까지 더듬는 숫자 여행은 흥미진진하지요. <숫자의 탄생>에서 뽑은 재미있는 숫자 상식 몇 가지를 시리즈로 소개합니다. <편집자 주>
손가락은 달랑 10개, 그럼 셀 수 있는 숫자도 10이 한계라고 생각하시죠? 그런데 그렇지 않았답니다. 놀랍게도 중국의 계산가들은 한 손으로는 10만까지, 두 손으로는 100억까지 헤아릴 수 있는 체계를 만들었대요! 한 번 살펴볼까요?
손가락으로 100억까지 헤아리기
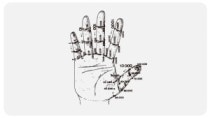
이 방식에서는 손가락 마디를 경계 짓는 각각의 관절이 왼쪽, 중앙, 오른쪽 접합부, 이렇게 세 부분으로 나뉜다. 그렇게 하면 각 손가락마다 십진법 순서에 따른 9개의 연속적인 단위가 있게 되는데, 오른손 새끼손가락은 한 자릿수, 약손가락은 10 자릿수, 가운뎃손가락은 100 자릿수, 집게손가락은 1 000 자릿수, 엄지손가락은 10 000 자릿수를 가리키고, 그다음 왼손의 엄지손가락이 10만 자릿수를, 집게손가락이 100만 자릿수를 가리키는 식으로 이어진다.
오른손 새끼손가락에서는 먼저 왼쪽의 위, 중앙, 아래의 세 접합부를 연속적으로 짚어 1에서 3까지 헤아린다. 그런 다음 가운데의 아래, 중앙, 위의 세 관절을 아래에서 위로 차례로 짚어 4에서 6까지 헤아린다. 끝으로 오른쪽의 위, 중앙, 아래의 세 접합부를 위에서 아래로 짚어 7에서 9까지 헤아린다. 오른손 약손가락에서도 이와 동일한 방식으로 셈을 해 먼저 10에서 30까지, 그다음 40에서 60까지, 마지막으로 70에서 90까지 헤아려 나간다. 오른손 가운뎃손가락에서도 같은 방식으로 셈을 해 100에서 900까지 헤아린다. 이하 동일. 이와 같은 방식으로 해 나가면 왼손 새끼손가락의 오른쪽 아래 관절에서 90억에 이르게 된다.
손가락으로 곱셈도 가능하다?
인간의 손은 단순히 셈을 하는 데만 머물지 않고 계산, 말하자면 여러 가지 산술 연산을 하는 데도 사용되었답니다. 다른 어떤 인위적 수단 없이 자신의 손가락으로 곱셈을 하는 것이죠. 이러한 전통은 인도, 이라크, 시리아, 세르비아, 북아프리카 등지에서 아직도 그 흔적이 남아 있다고 해요.
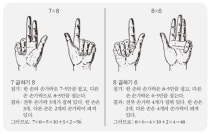
예를 들어 8×9를 하는 경우, 그 농부는 8에서 5를 뺀 나머지 숫자, 즉 8-5=3개의 손가락을 접고서 나머지 손가락 2개는 펼친 그대로 둔다. 그러고 나서 다른 한 손으로 9에서 5를 빼고 남는 만큼의 손가락, 즉 9-5=4개의 손가락을 접고서는 남는 손가락 하나를 펼친 그대로 둔다. 여기서 그는 먼저 양쪽 손의 접힌 손가락 수에 10을 곱하고(물론 암산으로)―이를 식으로 풀면, (3+4)×10=70이다―그런 다음 거기에다 첫 번째 손의 펼쳐진 손가락 수와 두 번째 손의 펼쳐진 손가락 수를 곱하여 생긴 결과―말하자면 2×1=2―를 더하여 얻고자 하는 곱셈의 결과를 얻는다. 이를 식으로 풀면 다음과 같다.
8×9=(3+4)×10+(2×1)=72
9×7을 하는 경우에도 그는 마찬가지로 첫 번째 손에서 9에서 5를 뺀 나머지 수만큼의 손가락, 즉 9-5=4개의 손가락을 접고, 다른 손으로 7에서 5를 뺀 나머지 수만큼의 손가락, 즉 7-5=2개의 손가락을 접는다. 이때 두 손의 접힌 손가락 전체 수에다 10을 곱하고―(4+2)×10=60―여기에다 한 손의 펼쳐진 손가락 수와 다른 한 손의 펼쳐진 손가락 수를 곱한 결과―1×3=3―를 더함으로써 목표로 한 곱셈 결과를 얻는다. 이를 식으로 풀면 다음과 같다.
9×7=(4+2)×10+(1×3)=63
고대인들이 분명 경험을 통해 알았을 이 방식은 틀리는 법이 없다. 이 방법을 쓰면 5와 10 사이에 있는 모든 수의 곱셈을 신속하게 해낼 수 있다.
<숫자의 탄생> p.133~136에서 인용 및 발췌, 정리
'부키 books~2012 > 숫자의 탄생' 카테고리의 다른 글
| 제로, 0은 과연 누가 발명했는가? - [숫자의 탄생]에서 가려 뽑은 숫자 상식 5 (0) | 2011.06.07 |
|---|---|
| 21세기에도 살아남은 가장 완벽한 계산도구는 - [숫자의 탄생]에서 가려 뽑은 숫자 상식 4 (0) | 2011.06.06 |
| 5진법, 10진법, 12진법, 20진법의 공통점은? - [숫자의 탄생]에서 가려 뽑은 숫자 상식 2 (0) | 2011.06.06 |
| 아이가 수를 셀 때 “하나 둘 넷”으로 셋을 건너뛰는 이유는? - [숫자의 탄생]에서 가려 뽑은 숫자 상식 1 (0) | 2011.06.03 |
| 공식이나 계산이 아닌 '이야기'로 수학에 접근하세요! - [숫자의 탄생] (0) | 2011.06.03 |
- Total
- Today
- Yesterday
- 비즈니스영어
- 부키전문직리포트
- 지난10년놓쳐서는안될아까운책
- 바버라에런라이크
- 교양과학
- 힘이되는한마디
- 가족의두얼굴
- 남회근저작선
- 가족에세이
- 문학·책
- 비즈니스·경제
- 힘이 되는 짧은 글귀
- 어학·외국어
- 부키 전문직 리포트
- 셰릴 스트레이드
- 셰릴스트레이드
- 자녀교육
- 김용섭
- 최광현
- 안녕누구나의인생
- 장하준
- 직업탐구
- 긍정의배신
- 심리에세이
- 진로지도
- 직업의세계
- 아까운책2012
- 와일드
- 남회근
- 영어
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
